Q) All triangles have a circum-circle, but not all quadrilaterals do.
Q) Another necessary and sufficient condition for a convex quadrilateral ABCD to be cyclic is that an angle between a side and a diagonal is equal to the angle between the opposite side and the other diagonal. That is, for example,
Q) Ptolemy's theorem expresses the product of the lengths of the two diagonals e and f of a cyclic quadrilateral as equal to the sum of the products of opposite sides:
Q) Ptolemy's Theorem Extension: In a cyclic quadrilateral the ratio of the diagonals equals the ratio of the sums of products of the sides that share the diagonals' end points. In other words, the ratio of the diagonals of any cyclic quadrilateral equals the ratio of the sums of the rectangles contained by the sides that share the diagonals' end points.
Q) If two lines, one containing segment AC and the other containing segment BD, intersect at X, then the four points A, B, C, D are con-cyclic if and only if
The intersection X may be internal or external to the circle. In the former case, the cyclic quadrilateral is ABCD, and in the latter case, the cyclic quadrilateral is ABDC. When the intersection is internal, the equality states that the product of the segment lengths into which X divides one diagonal equals that of the other diagonal. This is known as the intersecting chords theorem since the diagonals of the cyclic quadrilateral are chords of the circum-circle.
Properties:
1. If one side of the cyclic quadrilateral is produced, then the exterior angle so formed is equal to the interior opposite angle.
2. The sum of the opposite angles of a cyclic quadrilateral is supplementary.
3. If two opposite angles of a quadrilateral are supplementary, then it is a cyclic quadrilateral.
4. In a cyclic quadrilateral, the ratio of the diagonals equals the ratio of the sum of products of the sides that share the diagonal's end points.( Ptolemy's Theorem Extension)
5. Perpendicular Bisectors of a quadrilateral are concurrent only if it is a cyclic quadrilateral.
6. The four perpendicular bisectors of the four sides meet at the centre of the circle only if it is a cyclic quadrilateral.
7. If the sum of the measures of two opposite sides of a quadrilateral equals the sum of the measures of the two remaining opposite sides, then the quadrilateral is circumscribable. AB+DC = AD + BC; Example - Square, kite, rhombus, parallelogram, Rectangle.
Q ) In a cyclic quadrilateral ABCD the ratio of the diagonals equals the ratio of the sums of products of the sides that share the diagonals' end points. In other words:
| (1) | AC / BD = (AB·AD + BC·CD) / (AB·BC + AD·CD). |
Proof:
Triangles PAD and PBC are similar, so that
PA/PB = AD/BC = PD/PC,
which can be also written as
| (2) | AB·AD/PA = AB·BC/PB, and BC·CD/PC = AD·CD/PD, |
In the same manner, the similarity of triangles PAB and PDC implies
| (3) | AB·AD/PA = AD·CD/PD. |
which shows that four expressions
| (4) | AB·AD/PA, AB·BC/PB, BC·CD/PC, and AD·CD/PD |
are all equal. (1) follows by combining the first and the thrid terms and also the second and the fourth.
Q) The area K of a cyclic quadrilateral with sides a, b, c, d is given by Brahmagupta's formula
Q) If ABCD is a cyclic quadrilateral where AC meets BD at E, then:
Q) In a cyclic quadrilateral with successive vertices A, B, C, D and sides a = AB, b = BC, c = CD, and d = DA, the lengths of the diagonals p = AC and q = BD can be expressed in terms of the sides as:


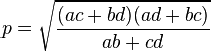
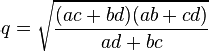
No comments:
Post a Comment